How to create binary search tree in javascript with ES6 classes

Intro

In this post, I'd like to share my implementation of Binary SearchTree (BST) in JavaScript using mechanism of ES6 Classes.

Binary Search Tree

Binary Search Tree is a node-based binary tree data structure which has the following properties: 1. The left subtree of a node contains only nodes with keys lesser than the node’s key. 2. The right subtree of a node contains only nodes with keys greater than the node’s key. 3. The left and right subtree each must also be a binary search tree. BST ref (geeksforgeeks)

class BinarySearchTree {
    constructor(data) {
    this.root = {
        data: data,
      left: null,
      right: null
    };
  }
  
  // Time complexity: 
  // In case of balanced tree: O(log N)
  // worst case O(n)
  insertTo(node, key) {
    if (key < node.data) {
        if (node.left) {
        this.insertTo(node.left, key);
        return;
      } else {
        node.left = new Node(key);
      }
    } else {
        if (node.right) {
        this.insertTo(node.right, key);
        return;
      } else {
        node.right = new Node(key);
      }
    }
  }
}

Node

class Node {
    constructor(data) {
    this.data = data;
    this.left = null;
    this.right = null;
  }
}

How to use it

let bst = new BinarySearchTree(0);

// add some nodes
bst.insertTo(bst.root, 2);
bst.insertTo(bst.root, 1);
bst.insertTo(bst.root, 3);
bst.insertTo(bst.root, 4);

Find element in BST

// Time complexity: 
// In case of balanced tree: O(log N)
// worst case O(n)
function findIn(node, key) {
  if (node.data === key) {
    return node;
  }
  
  if (key < node.data) {
    return node.left
      ? findIn(node.left, key)
      : null;
  } else {
    return node.right
      ? findIn(node.right, key)
      : null;
  }
}

Tree Traversals

Preorder

1. Visit the root.
2. Traverse the left subtree, i.e., call Preorder(left-subtree)
3. Traverse the right subtree, i.e., call Preorder(right-subtree)

Iteratinve method:

function preorder() {
  let currNode = this.root;
  let stack = [];
  stack.push(currNode);
  while(stack.length || currNode) {
    currNode = stack.pop();
    console.log(currNode.data);
    if (currNode.right) {
      stack.push(currNode.right);
    }
    if (currNode.left) {
      stack.push(currNode.left);
    }
  }
}

Recursive method:

function recursivePreorderTraversal(node) {
  if (node.data) {
    console.log(node.data);
  }
  
  if (node.left) {
    recursivePreorderTraversal(node.left);
  }
  
  if (node.right) {
    recursivePreorderTraversal(node.right);
  }
}

Inorder

1. Traverse the left subtree, i.e., call Inorder(left-subtree)
2. Visit the root.
3. Traverse the right subtree, i.e., call Inorder(right-subtree)

Iteratinve method:

function inorder() {
  let currNode = this.root;
  let stack = [];
  while(stack.length || currNode) {
    if (currNode) {
      stack.push(currNode);
      currNode = currNode.left;
    } else {
      currNode = stack.pop();
      console.log(currNode.data);
      currNode = currNode.right;
    }
  }
}

Recursive method:

function recursiveInorderTraversal(node) {
  if (node.left) {
    recursiveInorderTraversal(node.left);
  }

  if (node.data) {
    console.log(node.data);
  }
  
  if (node.right) {
    recursiveInorderTraversal(node.right);
  }
}

Postorder

1. Traverse the left subtree, i.e., call Postorder(left-subtree)
2. Traverse the right subtree, i.e., call Postorder(right-subtree)
3. Visit the root.

Iteratinve method:

function postorder() {
  let currNode = this.root;
  let stack = [];
  let lastVisited = null;
  
  while(stack.length || currNode) {
    if (currNode) {
      stack.push(currNode);
      currNode = currNode.left;
    } else {
      let peekNode = stack[stack.length - 1];
      if (peekNode.right && lastVisited !== peekNode.right) {
        currNode = peekNode.right;
      } else {
        console.log(currNode.data);
        lastVisited = stack.pop();
      }
    }
  }
}

Recursive method:

function recursivePostorderTraversal(node) {
  if (node.left) {
    recursivePostorderTraversal(node.left);
  }

  if (node.data) {
    console.log(node.data);
  }
  
  if (node.right) {
    recursivePostorderTraversal(node.right);
  }
}

Breadth-first search

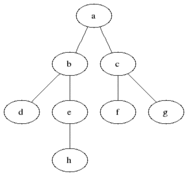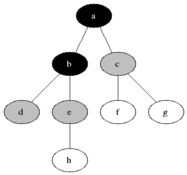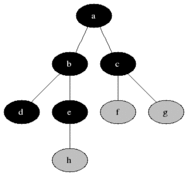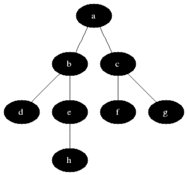
function breadth() {
  let currNode = this.root;
  let queue = [];
  queue.push(currNode);
  while(queue.length) {
    currNode = queue.shift();
    console.log(currNode.data);
    if (currNode.left) {
      queue.push(currNode.left);
    }
    if (currNode.right) {
      queue.push(currNode.right);
    }
  }
}

JSFiddle

<script async src="//jsfiddle.net/gudobw9n/11/embed/js/dark/">

Happy creating your own binary search trees! :)